Climatologarithme

Par MD

1/ Introduction.
Un récent article avait été consacré à l’analyse d’un graphique très illustratif extrait du « summary for policymakers » (SPM10) du dernier rapport du GIEC dit « AR6 ». Pour éviter les redites, on considérera cet article comme connu des lecteurs. En résumé, le GIEC postule une relation quasi-linéaire entre les émissions anthropiques cumulées de CO₂ depuis l’époque « préindustrielle » jusqu’à nos jours et l’évolution des températures. Il en tire une loi de proportionnalité dite TCRE (transient climate response to cumulative CO₂ emissions). Il extrapole cette loi pour simuler l’augmentation des températures dans le grand avenir selon plusieurs hypothèses de croissance (les « shared socieconoic pathways » ou SSP).
A titre de rappel, reproduisons à nouveau la figure SPM10 du GIEC.

2/ TCR ou TCRE ?
Le concept de sensibilité climatique est à la base de la doctrine traditionnelle du GIEC. A l’échelle décennale ou séculaire, la « transient climate response » (TCR) est définie comme l’augmentation de température censée résulter d’un doublement de la concentration en CO₂. Cette théorie a déjà été évoquée sur ce site. Lorsqu’un incrément est proportionnel à un rapport, la relation entre les deux variables est nécessairement logarithmique. Désignons la sensibilité TCR par S (°C), les températures par T (°C) et les concentrations en CO₂ par C (ppmv). Les valeurs initiales (dites « préindustrielles », année 1850) sont désignées par T₀ et C₀. En utilisant le logarithme binaire (lb, de base 2), on aurait ainsi :En effet si C/C₀ = 2 (doublement) on a bien lb (2) = 1 ; d’où T-T₀ (°C) = S * lb (2) ou encore : T-T₀ (°C) = S (°C).
Le concept de TCRE (transient climate response to cumulative CO₂ emissions) est très différent : il stipule que l’augmentation de température est une fonction linéaire des émissions anthropiques cumulées de CO₂ exprimées en masse (milliards de tonnes ou Gt).
Or on peut vérifier, selon le GIEC lui-même, que le rapport C/C₀ et les émissions cumulées évoluent parallèlement. Voici pourquoi.

3/ Emissions anthropiques cumulées ou rapport des concentrations ?
Le GIEC fait l’hypothèse fondamentale qu’une partie des émissions anthropiques est absorbée par des « puits » terrestres et océaniques. Il ne subsisterait donc dans l’atmosphère qu’une fraction atmosphérique (« airborne fraction »). Celle-ci est très variable selon les années, mais depuis environ 60 ans elle oscille autour de 44% (±10%) comme l’indique le GIEC (voir AR6, SPM A.1.1). C’est en effet ce que l’on peut constater au vu du graphique ci-dessous.Il en résulte que la masse de CO₂ (en Gt) dans l’atmosphère augmente linéairement avec le cumul des émissions anthropiques. Il en va de même de la concentration C (en ppmv) et du rapport C/C₀. On le voit sur la courbe ci-dessous, rigoureusement rectiligne pour les soixante dernières années (les variations annuelles sont atténuées du fait qu’il s’agit de cumuls). 
Lecture : en 1959, les émissions anthropiques cumulées depuis 1850 étaient de 747 GtCO₂. En 2019, de 2 411 Gt, soit 1 694 Gt de plus ; la concentration était passée de 316 à 412 (ppmv) soit 96 ppmv de plus ; et le rapport C/C₀ de 1,11 à 1,44.
Par conséquent, on peut indifféremment choisir comme variable « explicative » soit le cumul des émissions anthropiques de CO₂ (Gt) comme le fait le GIEC, soit le stock de CO₂ dans l’atmosphère (Gt), soit la concentration C de CO₂ (ppmv), soit enfin le rapport C/C₀ (concentration relativement à une valeur initiale).

4/ Choix de la période d’observation.
Dans ce qui suit, on se limitera à la période d’une soixantaine d’années pendant laquelle la fraction atmosphérique est réputée constante par le GIEC, soit depuis 1959, qui sera donc choisie comme nouvelle date de référence initiale. Il se trouve que cette date est aussi celle qui correspond au début des mesures directes de concentration en CO₂ à l’observatoire NOAA de Mauna Loa. Ces mesures sont reconnues au niveau international et sont probablement les plus fiables. On rajoutera les données pour 2020 et 2021, qui ne figuraient pas dans le rapport du GIEC.

5/ Evolution des températures.
Reprenons, en le limitant dans le temps, un graphique analogue à celui de l’article précédent. On a superposé les deux échelles (cumul des émissions anthropiques et rapport C/C₀). Les compteurs sont remis à zéro en 1959 (cumul = 0, C=C₀ et C/C₀=1). Notons que la température Hadcrut5 de 1959 prise cette fois comme origine est de 0,3°C au-dessus de celle de la « période préindustrielle » 1850-1900.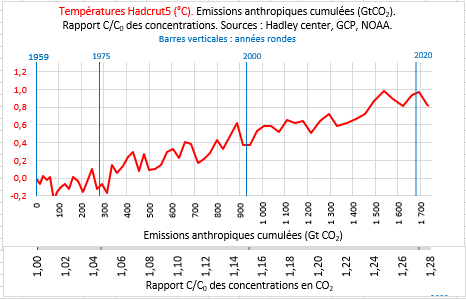

6/ Linéaire ou logarithmique ?
On peut compléter le graphique précédent en lui superposant le modèle linéaire TCRE du GIEC (soit +0,45°C pour 1 000 GtCO₂) représenté par la droite verte.On voit que le modèle simule tant bien que mal l’évolution des températures de 1959 à 2021.
Mais on pourrait faire une autre simulation, en adoptant cette fois une fonction logarithmique, et en essayant par tâtonnement de la rapprocher de la fonction linéaire. On trouve que la valeur adéquate de sensibilité (TCR) serait S = 2,2°C (cette valeur se situe à l’intérieur de la fourchette traditionnellement retenue). La fonction s’écrirait donc : T-T₀ = 2,2 * lb (C/C₀), représentée par la courbe violette surajoutée au graphique précédent.Sur la période considérée, les deux simulations sont pratiquement confondues. Au-delà, les courbes commenceraient à diverger lentement, comme on le voit ci-dessous dans l’exemple du scénario médian SSP2-4.5, la fraction atmosphérique étant supposée se maintenir à 44%. Ce n’est qu’une simple illustration sur laquelle on ne s’appesantira pas.La différence est certes modeste et reste dans les fourchettes d’incertitudes. Mais on sait que la science officielle scrute le moindre dixième de degré en plus ou en moins et en tire bruyamment toutes sortes de conséquences.

7/ Conclusion.
Précisons que le présent exercice doit être considéré comme une simple distraction mathématique. Il ne s’agit pas de substituer un « modèle » au « modèle » officiel. D’ailleurs rien n’interdirait de tester d’autres fonctions algébriques de degrés variés qui pourraient tout aussi bien (ou aussi mal) « coller » avec les observations de la période 1959-2021.
Les deux fonctions envisagées ici, que l’on sache, ne reposent aucunement sur des lois physiques indiscutables ; ce ne sont que des formules empiriques voire purement visuelles plaquées sur des données factuelles. Les extrapoler à des horizons éloignés n’en est que plus hasardeux.

Publicité